2.1
1
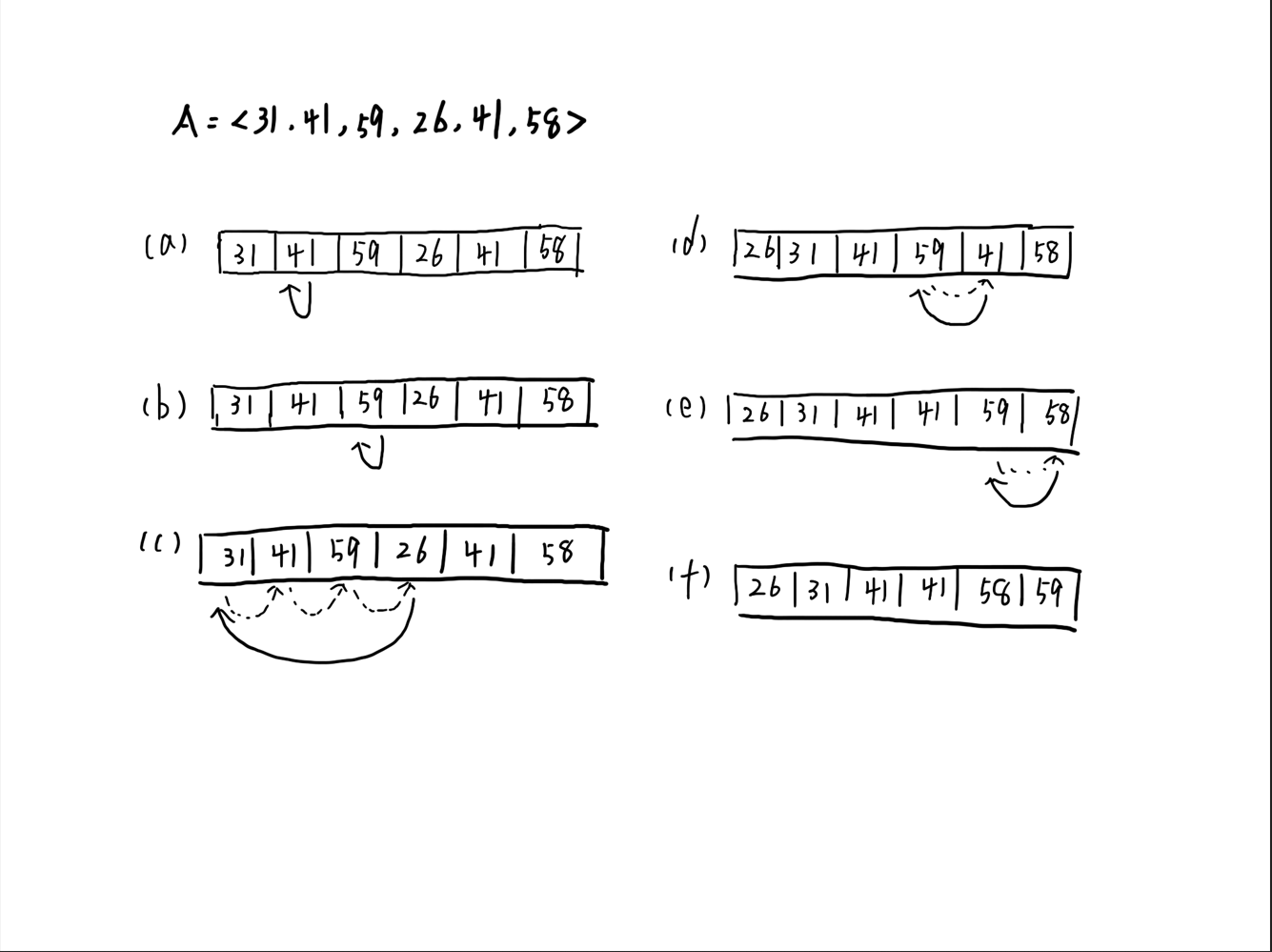
2
INSERTION-SORT(A)
for j = 2 to A.length
key = A[j]
i = j-1
while i>0 and A[i]<key
A[i+1]=A[i]
i=i-1
A[i+1]=key
3
for i = 1 to A.length
if A[i]=v
return i
v = NIL
A[1..i-1]表示位置1到i-1的元素都不等于v
**初始化:**当i=1时,没有元素,自然也没有元素等于v
**保持:**每次循环会将不等于v的元素加入到A[i..i-1]中
**终止:**如果遇到A[i]=v,循环终止。如果最后i=A.length时,A[1..i-1]中元素都不等于v也就是数组中所有元素都不等于v。
4
**输入:**两个二进制序列
$$A=<a_1,a_2,\cdots,a_n>,B=<b_1,b_2,\cdots,b_n>$$
**输出:**二进制序列
$$C=<c_1,c_2,\cdots,c_n,c_n+1>,C=A+B$$
carry = 0
for i = n downto 1
C[i] = A[i]^B[i]^carry
if(A[i]+B[i]+carry>1)
carry = 1
else
carry = 0
c[1] = carry
2.2
1
$\theta(n^3)$
2
for i = 1 to A.length-1
min = i
key = A[i]
for j = i+1 to A.length
if A[j]<A[min]
min = j
A[i] = A[min]
A[min] = key
**循环不变式:**A[1..i]表示数组中已经排序序的部分并且A[1..i]的任意数字不大于未排序部分的数字
因为A[1..i]部分的数字一定不大于未排序部分的数字,所以当未排序的部分只剩一个数字时,该数字一定为最大值。
选择排序的最好情况和最坏情况相同,每一个元素都要与剩下的所有元素做比较才能选出最小值。
$$\begin{align*} C(n)&=(n-1)+(n-2)+(n-3)+\cdots+1\ &=\frac 1 2(n-1)n\ &=\frac 1 2n^2-\frac 1 2n \end{align}$$
时间复杂度为$\theta (n^2)$
3
第n个位置的元素为要查找的元素,查找次数为n
$$\begin{align*} C(n)&=\frac {(1+2+3+\cdots+n)} n\ &=\frac {\frac 1 2(n^2+n)} n\ &=\frac {n+1} 2 \end{align*}$$
平均查找次数为$\frac {n+1} 2$
最坏查找次数为$n$
平均情况和最坏情况的时间复杂度都为$\theta(n)$
2.3
1
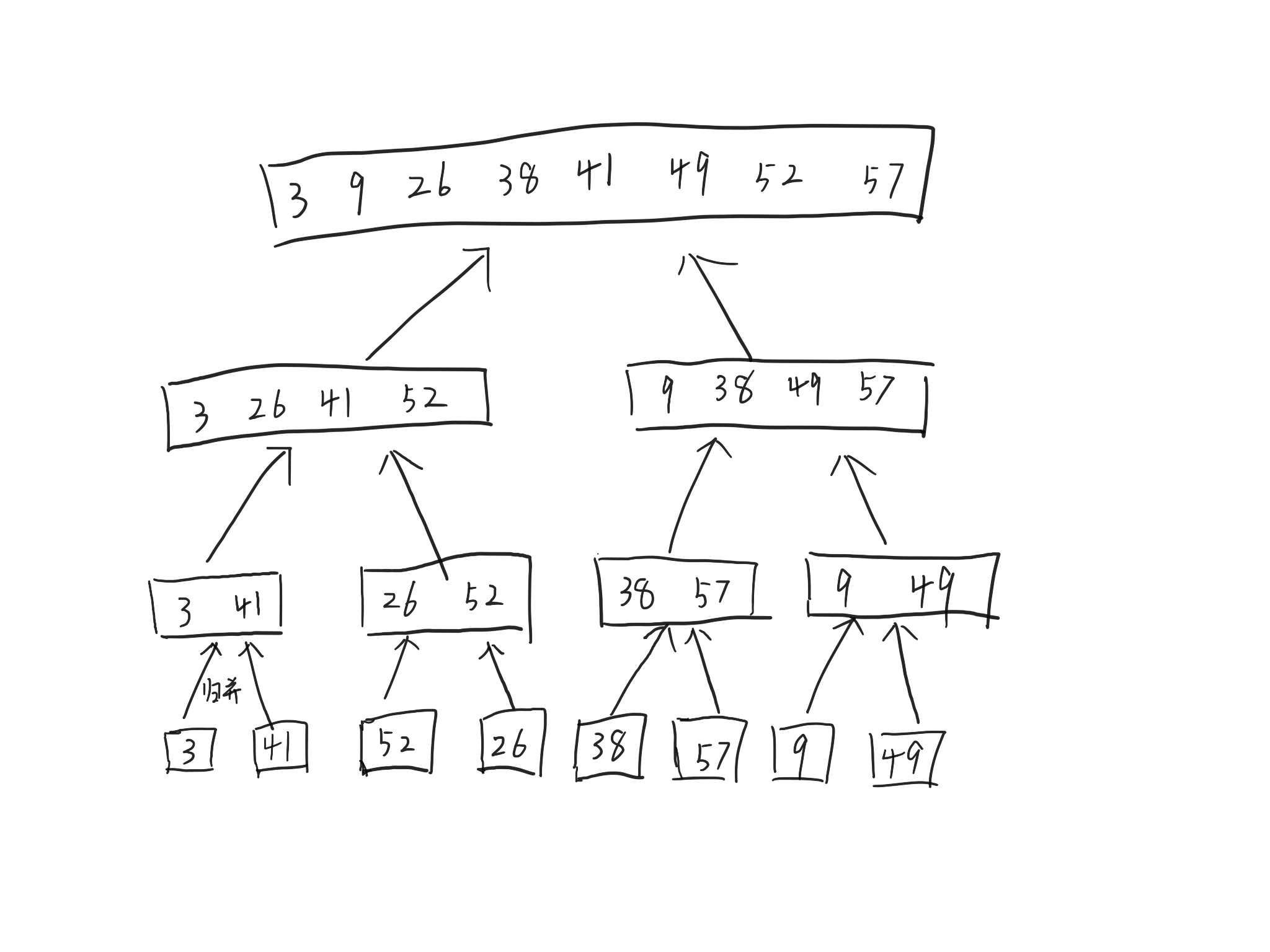
2
MERGE(A,p,q,r)
n1 = q-p+1
n2 = r-q
let L[1..n1+1] and R[1..n2+1] be new arrays
for i = 1 to n1
L[i] = A[p+i-1]
for j = 1 to n2
R[j] = A[q+j]
i = 1
j = 1
k = p
while i <= n1 and j <= n2
if L[i]<= R[j]
A[k] = L[i]
i = i+1
else A[k] = R[j]
j = j+1
p++
while i <= n1
A[k] = L[i]
k++
while j <= n2
A[k] = R[j]
k++
3
当n=2时,$T(n)=2$,命题成立
假设当n=m时,命题成立,即
$$\begin{align*} &T(m)=mlgm\
\end{align*}$$
则当n=2m时
$$\begin{align} T(2m)&=2T(2m/2)+2m\ &=2T(m)+2m\ &=2(T(m)+m)\ &=2(mlgm+m)\ &=2m(lgm+1)\ &=2mlg2m \end{align}$$
所以,当$n=2^k$时,递归式的解时$T(n)=nlgn$
4
$$T(n)=\begin{cases}1&n=1\T(n-1)+(n-1)&n>1\end{cases}$$
5
BINARY_SEARCH(A,key)
i = 1
j = A.length
while i<=j
mid = (i+j)/2
if A[mid]=key
return mid
else if A[mid]>key
i = mid+1
else
j = mid-1
return NIL
$$\begin{align} &T(n)=T(n/2)+\theta(1)\ &T(n)=\theta(lgn) \end{align}$$
6
INSERTION-SORT(A)
for j = 2 to A.length
key = A[j]
l = 0
r = j
while l+1!=r
do mid<-(l+r)/2
if A[mid]>=key
r = mid
else
l = mid
A[j]=A[r]
A[r]=key
7
- 将$S$排序
- 将集合$P={z:z = x-y,y\in S}$排序
- 删除集合$S和P$中的重复元素
- 合并集合$S和P为Q$
- 如果$Q$中有重复元素,那么集合$S$中有和为$X$的两个元素
思考题
1
**a.**插入排序排序长度为$k$的子表最坏情况为$\theta (k^2)$,排序$n/k$个子表的最坏情况为$\theta (k^2 \times \frac {n} {k})=\theta (nk)$
**b.**用归并的思想合并,每一层的合并最坏情况需要$\theta (n)$,一共有$\theta (lg(n/k))$层,所以最坏情况为$\theta (nlg(n/k))$
c.$\theta (lgn)$
*d.*k为插入排序比归并排序更快的最大长度
2
a. 序列A是无序的 序列A’中的元素是序列A中原来的元素的排序
b.
循环不变式:$A[j]是序列A[j..n]中最小的,并且A[j..n]是原来A[j..n]的一个排序$
**初始化:**循环开始的时候$j=A.length$,所以$A[j]是序列中最小的$
保持: 进入循环后,如果$A[j-1]>A[j]$,那么就交换$A[j-1]和A[j]$的值,否则采取行动,接着$j$自减1,$A[j-1]$加入序列$A[j..A.length]$,$A[j-1]$还是序列中最小的,并且组成元素没有发生改变
结束: 当$j=i$时循环结束,此时$A[i]$是序列$A[i..A.length]$中最小的
c.
循环不变式:$A[1..i-1]中是原序列中最小的i-1个元素并且已经排序,A[i..n]是剩余的n-i+1个元素$
初始化:$i=1,A[1..i-1]为空$
**保持:**内部循环每次结束之后,$A[i]是剩余的元素中最小的元素$,所以$A[1..i-1]中会添加最大的元素里面最小的元素,即A[1..i-1]是有序的,并且元素都是原来的序列中的$
**结束:**当$i=A.length$时,循环结束,此时$A[1..n-1]中时有序排列的元素$,$A[n]$比其他所有元素大,所以整体的序列时有序的
d.
$$\begin{align} C(n)&=(n-1)+(n-2)+\cdots+1\ &=\frac {n(n-1)} {2}\ &=\frac {1} {2} n^2 - \frac {1} {2}n \end{align}$$
冒泡排序的时间复杂度都是$\theta(n^2)$
而插入排序最坏时间复杂度是$\theta(n^2)$,最好的情况是$\theta (n)$
3
a. $\theta(n)$
b.
y = 0
for i = 0 to n
z = a[i]
for j = 1 to k
z = z*z
y = y+a[k]*z
朴素算法的时间复杂度为$\theta (n^2)$
c.
循环不等式:$y=\sum\limits*{k=0}^{n-(i+1)}a*{k+i+1}x^k$
**初始化:**刚开始的时候没有项,$y=0$
保持:
在某次循环开始之前,循环不等式成立,即
$$\begin{align} y=\sum\limits_{k=0}^{n-(i+1)}a_{k+i+1}x^k \end{align}$$
进入循环体后,执行第3行代码后,有
$$\begin{align} y&=a_i+x\cdot\sum\limits_{k=0}^{n-(i+1)}a_{k+i+1}x^k\ &=a_i+\sum\limits_{k=0}^{n-(i+1)}a_{k+i+1}x^{k+1}\ &=a_i+(a_{i+1}x+a_{i+2}x^2+\cdots+a_{n}x^{n-i})\ &=\sum\limits_{k=0}^{n-(i+2)}a_{k+i+2}x^k \end{align}$$
当i自减1进入下一次循环后,循环不等式依旧成立
结束:
当i=-1时,循环结束,此时$y=\sum\limits*{k=0}^{n}a*{k}x^k$
d.
由**c.**可知
4
a. $(1,5),(2,5),(3,4),(3,5),(4,5)$
b.
降序排列的数组拥有最多的逆序对
$$\begin{align} C(n)&=(n-1)+(n-2)+\cdots+1\ &=\frac {n(n-1)}{2} \end{align}$$
c.
正比
对于任意一个需要待插入到正确位置的元素$A[i]$,逆序对$(j,i),j<i$的数目就是$A[i]$需要比较的次数,并且当元素$A[i]$插入到正确位置之后以该元素为第一个元素的逆序对的数量并没有发生变化
d.
class Solution {
vector<int> aux;
public:
int reversePairs(vector<int>& nums) {
aux.resize(nums.size());
return mergeSort(nums,0,nums.size()-1);
}
int merge(vector<int>& nums, int l, int m, int r){
int cnt = 0;
for(int i = l;i<=r;i++){
aux[i]=nums[i];
}
int p1 = l;
int p2 = m+1;
int index = l;
while(p1<=m&&p2<=r){
if(nums[p1]<=nums[p2]){
aux[index] = nums[p1];
p1++;
index++;
cnt+=p2-(m+1);
}else{
aux[index] = nums[p2];
p2++;
index++;
}
}
while(p1<=m){
aux[index++]=nums[p1++];
cnt+=p2-(m+1);
}
while(p2<=r){
aux[index++]=nums[p2++];
}
for(int i = l;i<=r;i++){
nums[i]=aux[i];
}
return cnt;
}
int mergeSort(vector<int>& nums, int l,int r){
if(l>=r){
return 0;
}
int m = l+(r-l)/2;
int cnt = mergeSort(nums,l,m)+mergeSort(nums,m+1,r);
return cnt+merge(nums,l,m,r);
}
};